At least once in every computer engineer's life, the question must arise,
"Can I create the illusion of a chord in QuickBASIC by rapidly multiplexing different notes on my internal PC speaker?"
Well, OK, maybe not that question exactly. But a lot of engineers can probably attest to having a craving for solving tough problems with limited tools, and since I have a passion for both music and retro computers, this was my chosen challenge last weekend.
As a little background, QuickBASIC is the simple language/compiler that came bundled with MS-DOS back in the day. It's the distant ancestor of the Visual Basic many of you may know now and Microsoft's replacement of the older GW-BASIC which arguably first exposed programming to the masses (perhaps with the exception of Applesoft BASIC of Apple II fame).
QuickBASIC lets you do a lot of fun stuff with your computer (i.e. graphics and sound) with just a couple lines of code. Like the Arduino of the 80's.
So in my search for the lost chord (yeah, Moody Blues reference), naturally I returned to this glorious language where I first cut my teeth on programming. I won't bore you with the bulk of the code, but here's what the important stuff looks like:
SUB PlayChord (SomeChord AS Chord, Duration, MultiplexingDuration) ' Convert from seconds to clock ticks. LocalDuration = 18.2 * Duration LocalMultiplexingDuration = 18.2 * MultiplexingDuration ' Compute local values. NumIterations = LocalDuration / LocalMultiplexingDuration NumNotes = SomeChord.NumNotes NoteDuration = LocalMultiplexingDuration / NumNotes ' Play the notes. FOR i = 1 TO NumIterations SOUND SomeChord.Note1, NoteDuration IF (SomeChord.NumNotes >= 2) THEN SOUND SomeChord.Note2, NoteDuration IF (SomeChord.NumNotes >= 3) THEN SOUND SomeChord.Note3, NoteDuration END IF END IF NEXT i END SUB
where a chord is defined as below:
TYPE Chord NumNotes AS INTEGER Note1 AS INTEGER Note2 AS INTEGER Note3 AS INTEGER END TYPE
Each integer in the chord represents the frequency of the given note. I also added a NumNotes member to give us the option of experimenting with different numbers of simultaneous notes. Pretty simple.
Sure we could improve the scalability of the code, but this isn't a programming exercise, and frankly, this beginner's language from 1985 doesn't exactly make arrays embedded in custom types easy. Our goal here is to make music, so let's get started….
I start with a simple G major chord:
DIM Gmaj AS Chord Gmaj.NumNotes = 3 Gmaj.Note1 = 196 Gmaj.Note2 = 247 Gmaj.Note3 = 294
which sounds like this with a "multiplexing duration" of 0.02:
Note that the "multiplexing duration" effectively defines how long each note in the chord should be played. So if we increase the multiplexing duration, we should expect to hear the individual notes in the chord become clearer and clearer:
While the higher mux durations give us that cool arcade sound we all know and love, the 0.02 mux value clearly masks the multiplexing best, producing a sound closest to anything we could consider a chord.
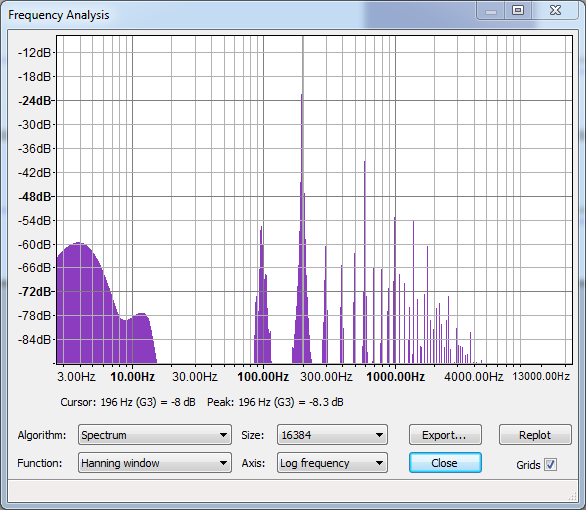
However, the short note durations of the first track yield a distinctly "dirty" sound that's not too appealing. Taking a closer look in Audacity's Frequency Analysis, we can see why:
Whoa! That's a lot of extra frequencies that we really don't want. For reference, this is what the chord looks like if we set NumNotes to 1 and just play the G note:
Much cleaner.
OK, so what's happening in the first plot (the triad G major chord) that's giving us all of those bogus frequencies, and how bad is it really? Well, let's take a closer look at the magnitudes of each of those frequencies by exporting the data to Excel:
| Frequency (Hz) | Level (dB) |
|---|---|
| 277.240 | -13.598 |
| 242.249 | -13.975 |
| 242.249 | -14.027 |
| 193.799 | -15.295 |
| 193.799 | -15.356 |
| 290.698 | -15.501 |
| 290.698 | -15.592 |
| 223.407 | -16.158 |
| 220.715 | -16.636 |
| 279.932 | -16.692 |
OK, so while this provides some clarity—note that we can see frequencies near the three expected ones: 196, 247, and 296—it also raises a couple interesting, perhaps related, questions:
- Why do each of the three primary frequencies come out a little flat (slightly lower) than what they should be?
- What is this unexpected 277-Hz frequency doing at the top of the chart??
Well, to help us better understand what's going on, let's take a look at the data for the 0.08 mux duration (i.e. longer notes):
| Frequency (Hz) | Level (dB) |
|---|---|
| 247.632 | -17.319 |
| 296.082 | -17.467 |
| 196.490 | -18.709 |
| 244.940 | -18.968 |
Alright, now that looks a little better. This tells us that when the notes are played for a longer period of time, not only do they come out closer to the expected frequencies, but they also appear as the three loudest frequencies in the spectrum.
So it appears from the data (granted from only two data points) that the accuracy of the notes depletes as their duration decreases.
As it turns out, when the notes are short enough, it doesn't appear that there is enough time to generate a strong consistent tone free of aberrations:
In this waveform view of the 0.02 mux chord, the issue is painfully obvious: the G note—the root note of the chord—is too low of a frequency to be played in the small time slice allotted to each note in the chord. The time slice is so small in fact that only one cycle of the note can by played, effectively resulting in no audible note.
Upon closer inspection, we can account for the specific reason why the frequency 190 Hz appears stronger than the expected frequency of 196 Hz: the transition from the D note to the G note is slightly longer than the pulse width of the G note itself (i.e. one half of 1/196 seconds). This slightly longer duty cycle is what yields the flat G and is likely what causes the other flat notes as well.
The final big issue is the inconsistency between note transitions. If you choose any note transition (e.g. B to D) and then look for the same transition later in the waveform, you'll likely find that the duration of the transition is slightly different. While this discrepancy might seem trivial on the scale of microseconds, our ears (as well as our software) is sensitive enough to pick up the difference, and it's these little discrepancies that are likely resulting in the unwanted extra frequencies in our chord.
Unfortunately, the transition consistency problem is far from trivial: because commands sent to the PC speaker are interrupt-driven, using these high-level constructs for generating sounds results in fairly non-deterministic behavior. To gain full control, we need lower-level code (i.e. assembly) that can manipulate the PC speaker directly. This of course, is a whole other blog entry—and probably entire project—altogether.
For reference, there is a lot of information and previous work out there for playing full-fledged WAV-like music through the PC speaker that completely blows this effort out of the water. Check out this example if you're interested: