Since purchasing my function generator, I've been doing a lot of thinking about what kinds of creative projects I can accomplish with this seemingly simple device.
One concept that struck me almost immediately was using the Voltage Controlled Frequency (VCF) input of the function generator to vary the sound via some external source, and since I'm a guitar player, naturally I looked to my guitar as the ideal controller.
This isn't a very new idea. In fact, the Roland GR-55 puts to shame pretty much any hypothetical device I could imagine:
Clearly something of that caliber is out of my ballpark, but I might be able to achieve something simpler.
My idea (again, nothing incredibly novel) is to use a simple Frequency Controlled Voltage (FCV) chip to convert my guitar signal to a specific voltage and then provide that to the function generator's VCF input. The ideal result would be a clean synth sound coming straight from my guitar.
The reality of course is much more complicated.
Unfortunately, the function generator is monophonic: it is only capable of playing one "note" at a time. So it's imperative that whatever voltage input I provide it is a clean representation of a single guitar note rather than the complex assortment of frequencies that are present in an actual guitar's sound. This is no trivial problem. Even if I focus on plucking only a single string, a single note is actual comprised of a variety of overtones that pollute the sound and could potentially distract the circuitry from the fundamental frequency:
Plucking the open D string of a Fender Stratocaster
So the next thought is, "Well, that's OK: I'll just pass the signal through a few band pass filters and choose the band with the maximum output as my fundamental frequency." While that may sound like a perfectly simple solution to the problem, this is where things get much harrier. Let's take a look at the spectrum of frequencies that are actually comprising this signal:
Ouch. Take a look at that. The fundamental frequency of our D3 note, approximately 147 Hz, isn't even the peak frequency in the spectrum! To be fair, we have to pay attention to the fact that of all of the partial frequencies, the group of tones around the D3 clearly have the largest area; therefore, that collection of closely aligned frequencies will together cut through the mess to create what we perceive as a single D.
If only band pass filters worked like human ears….Look what happens when we try to cut a slice out of the spectrum that should represent a D3 note (144 to 150 Hz):
Top: original complete guitar D note. Bottom: Extracted frequencies in the range of 144-150 Hz.
What?? Things certainly aren't looking good here. The extracted range (D3) is of such a low volume, it's hard to believe that we could even categorize the original signal as a D at all. And if we were to expand the band any wider, we'd start to pick up the surrounding notes (C# and D#) and in turn detract from the cleanliness of our signal.
To put it simply, reducing a raw analog guitar signal—even just one note—to a single frequency that can be cleanly converted by an FCV chip may require some more advanced circuitry.
However, there is a bit of hope: if you look carefully at the figure above, you'll notice that the smaller signal at the bottom representing the D3 note has a period that directly aligns with that of the big spikes in the top signal. This could be very good news: if the FCV chip can trigger on peaks, it will accurately detect the fundamental frequency and provide the single voltage we need.
Unfortunately I'll need to do more investigation into the problem before I have a complete answer (for another blog post). But in the meantime, while we're in the business of deconstructing guitar signals, I thought it would be a fun wrap-up to work our way back up to that original dirty signal from scratch.
In referring to the frequency spectrum shown above, I chose the ten loudest frequencies and combined them in Audacity to produce an artificial guitar sound:
Artificial guitar D3 note: 10 simple sine waves and a single additive composite.
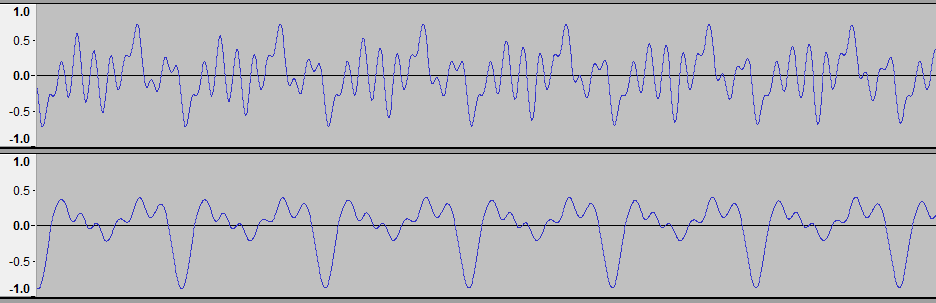
Comparing the resulting composite wave to the original actual guitar sample, we can see that the synthesis isn't that far off:
Top: artificial guitar. Bottom: actual guitar
The primary sources of difference between the two waves is merely the magnitude of each of the partial frequencies, which for the sake of simplicity, I kept nearly the same across the entire spectrum. This shortcut results in "fuller" bands (louder notes), such as the D3, being underrepresented and "narrower" bands (softer notes) being overrepresented.
Here are the audio samples of the two different waves: