Building on my last post regarding a cleaner way to use threads in C++, I decided to see what kind of performance I could expect out of these "threaded objects." My experiments ended up being more of an exploration of threads themselves than my specific implementation of them, but the results were nonetheless quite interesting.
What I found wasn't all that surprising—the overhead of swapping threads in and out of context is constantly drilled into the head of any computer engineer—but getting a first-hand look at the performance implications certainly puts that concept into perspective.
I wanted to start things off by understanding what kind of cost I incur from the "multithreadedness" alone, so I designed the threaded function to do one simple operation and then return: that way, I can mostly rule out irrelevant cycles and instead focus on the operating system's management of the threads by itself.
Note that here, I consider a "job" to be a block of work that is assigned to a thread (i.e. a workload).
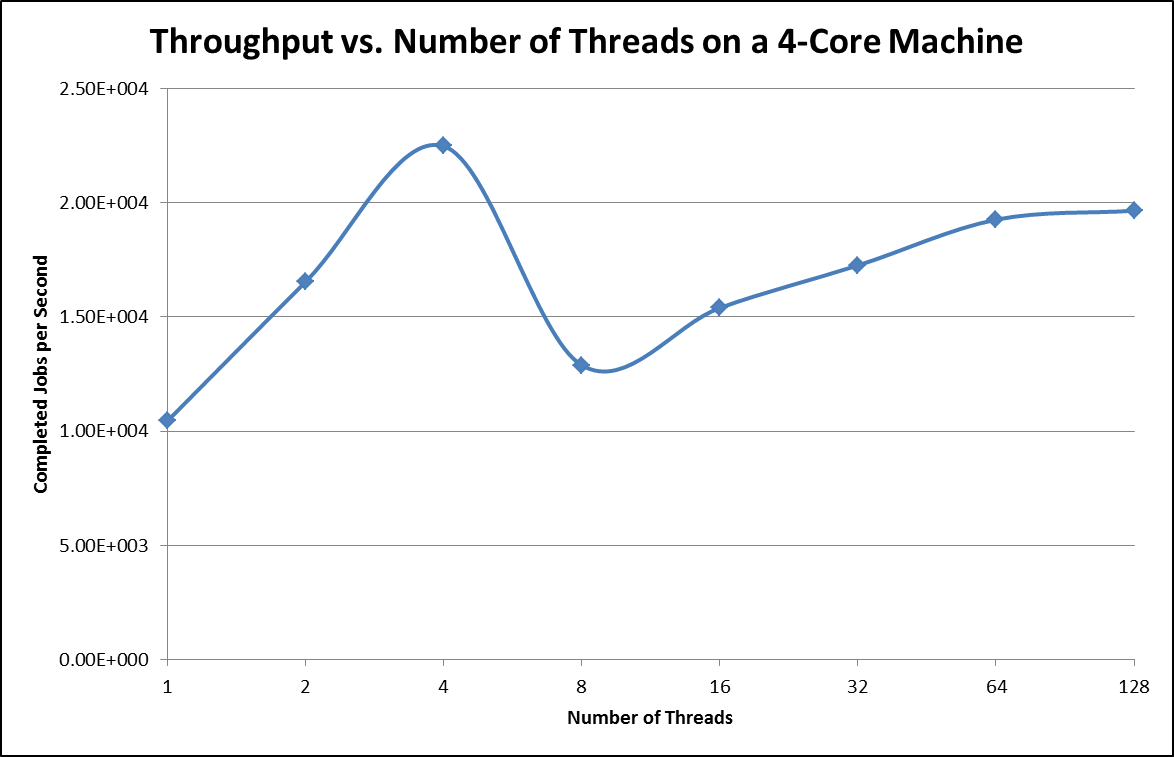
As you can see in the chart above, not surprisingly, the optimum number of threads available to the program is that which aligns perfectly with the number of cores on the system. Anything less, and the cores aren't being fully utilized. Anything more, and threads are left waiting in a queue to be swapped into context. The data does imply that there is some asymptote that may approach the performance of 4 threads, but why waste resources achieving what you can do with much less memory?
Oh yeah, this is why.…
Since in the first experiment we were only trying to capture the overhead of multithreading, we weren't letting the threads perform any real work and show off their stuff. Here in this data though, we give the threads something to do by varying the number of "iterations" contained in each job (just a useless loop with some foobar math).
As you can see, and again, as you'd expect, the longer the job is, the more useful multithreading becomes; essentially, with long jobs, the time saved through parallelizing the "user" portion of the program overshadows the time lost through the overhead of the "system" portion (managing the threads at the kernel level).
So this data is great and all, but what do we do with it? I see a couple of key intersections and inflection points that could be useful in designing a program, but how do I make this information general enough to be apply it to my design?
Well, the two terms I used above—"user" and "system"—were actually used with good reason. Through my experimentation I found a very handy C function called getrusage, which provides me with a lot of really cool details about how my program is operating under the hood—including a breakdown of its CPU time between "user" space and "system" space. The idea was that if I could use this function to get solid (consistent) numbers for user time and system time, I could find a pattern that would give me some insight into how to generalize this information.
So to find this pattern I returned to the original experiment, measuring only thread-related overhead and ignoring the cost of the user code. Since the test was designed to stress thread management alone, the curve of system time per thread followed the original (total time) curve exactly (but as an inverse, since we're measuring time rather than throughput):
Now we have a sense of how much time it takes to manage a thread during its lifetime—let's say about 100 microseconds to make the math easy.
So what's next? Well, now we need to go back to the second experiment—evaluating the usefulness of multithreading for varying lengths of jobs. Again, here, I can see a couple of key points:
Point A is important because it marks the point at which the job is long enough to make a threaded program at least equal throughput of a sequential program doing the same job. Beyond that point, and multithreading is always better. Point B is our second interesting point because it marks the point at which the marginal throughput benefit of using 128 threads instead of only 4 is so small that it may not justify the additional resources it requires.
Now, if we take a look at the user time for programs at these two points, we should be able to get a quantifiable sense (in seconds) of how long a job needs to be in order to make use of threads.
What I found is that, for this specific kind of job, the sequential program was in user space for about 0.361 microseconds per iteration. That means that a sequential program at Point A is in user space for about 18 milliseconds, and a sequential program at Point B is in user space for about 3600 milliseconds.
But we're still lacking some generalization: how do these results to scale to another processor, another operating system, or even a system busy working on other (unrelated) processes at the same time? What we need is a way to remove the units from this data—a ratio.
The table below showing the ratio of user time to system time, when compared to the data in the second experiment, demonstrates a clear positive correlation between the "user:system" ratio and the throughput of the particular configuration.
From this data, we can gather that a user-to-system ratio greater than 2 is a reasonable lower threshold for estimating that parallelizing a program (of this style) with threads will provide a throughput benefit.
The upper threshold is interesting as well: the data suggests that at some point between 1,000,000 and 10,000,000 iterations per job, the user:system ratio of the 4-thread program and the 128-thread program converge, perhaps in the neighborhood of 5,000,000 iterations, slightly before Point B on the graph. In fact, if we look at the graph closely, we can see that indeed there appear to be two opposing inflection points on the 4-thread and 128-thread curves at precisely that point.
So where does all of this information leave us? Well, it gives us a framework for evaluating the throughput potential of parallelizing a sequential program. Of course, in order to accurately determine this potential, we need to gather some rough time measurements on a case-by-case basis. But once we have that user and system data for a given operating system and machine, it should be relatively straightforward to cross-reference the resulting user:system ratio with the results shown above to correctly size the number of threads allotted to the program.
OK, so what are we leaving out here? Well…frankly, a lot. The jobs that we were analyzing were extremely straightforward arithmetic with minimal data dependencies and practically no memory footprint of any real significance. What happens when we try these methods with lots of data dependencies—say traversing a tree? Or perhaps even more importantly, what happens when the same program is run in a different environment? Will our optimizations still be optimum?
To make this a true general solution, there needs to be some underlying automated intelligence to the design. One could imagine an API that decides internally how many threads to use for the jobs, if any at all, based on what it has learned from trying a variety of solutions in recent runtime history.
Even this "automated solution picker" method has its pitfalls: for instance, non-standard jobs break the "learning" concept pretty quickly, but those may just be corner cases, especially if the designer is considering that the jobs are uniform enough to parallelize in the first place. Perhaps more important would be ensuring that the overhead to attempt different solutions and pick the best one wouldn't be large enough to impact the performance of the program.
Hopefully in the future I'll have a chance to test out some of these concepts (or research existing solutions).